RETURN TO ODDS AND ENDS INDEX

The signal to noise ratio quantifies how well an object like a star say can be distinguished from the noise in an image. Signal to noise ratio is a more important measure than pure sensitivity or gain. A sensitive camera is of no value unless it has low enough noise to allow that sensitivity to be useful.

To understand the way stacking can improve the signal to noise ratio in an image, we need first to understand the various sources of noise in a CCD image and how they affect the final result.

Our starting point is the equation for the ratio of the signal to noise for the camera. This is from the Roper Scientific Photometrics website

Signal to Noise Ratio (SNR) = ---------------------(1)

where:

I = Photon flux (photons/pixel/second)
QE = Quantum efficiency
t = Exposure time (seconds)
Nd = Dark current (electrons/pixel/sec)
Nr = Read noise (electrons)

Note that this equation describes the effects for an individual pixel.

This equation contains a lot of information about the various noise sources and is worth breaking down so we can understand exactly what is happening when a CCD image is recorded.

On the top of the equation we have I QE t , which is the signal produced by the star or other object. The photons which fall on the pixel in one second are converted to a number of electrons, depending on the Quantum Efficiency. This number is multiplied by the exposure time t to give the total number of electrons produced by the star during the exposure.

On the bottom of the equation are all the sources of noise; those effects which cause the signal to vary from its true value.

The variability of something is measured by its standard deviation SD (sometimes called the RMS error) If a random variable has a mean value of say 10 and a standard deviation of 2, then you would expect that 95% of the time, the value would lie within +-2SD ie between 6 and 14. To find the total variability from all sources of noise, you have to square the standard deviations of each noise source, add them together and then take the square root of the total. This is why the terms on the bottom are added together inside the square root sign.

The first term is I QE t again ie the number of electrons produced by the light from the star. How can this be producing noise?

Well, the photons from the star do not arrive at regular intervals but in fact turn up randomly. For example if you measure for 5 seconds the number of photons arriving from a star which is producing say 20 photons per second, you might get only 93 photons one time and perhaps 112 on another occasion. This is called shot noise. It means that even an image from a perfect camera will have noise due to the random nature of starlight.

The interesting thing about counting objects like this which are random in their behaviour is that the variability is directly related to how many you count on average. The standard deviation is the square root of the number counted,

which in this case =

This is squared to produce the first noise term in the equation.

It is interesting to see what happens to shot noise as the number of photons counted increases, either because the object is brighter or by taking a longer exposure.

If we count 10 photons on average, the standard deviation is = 3.16 or 31.6% of the mean

If we increase the number counted to 100, the standard deviation is now 10 or only 10% of the mean.

The second term is the dark noise. This is produced by extra electrons generated in the CCD which are not caused by the photons. These accumulate randomly during the exposure to produce a dark current, proportional to the exposure time. (Note that this is different to any DC bias caused by the voltages in the electronics not being exactly in balance. The latter should not vary and would be a fixed value, independent of the exposure time.)

In exactly the same way as the shot noise is calculated, the standard deviation of the dark noise is given by which is then squared to produce the second noise term in the signal to noise ratio equation.

Note that the main source of dark noise is thermal electrons which are a function of temperature. The dark noise can be reduced by reducing the temperature of the CCD

The third noise term in the equation is read noise. This is additional noise generated by the electronics as when the CCD is read out. Because it is not a statistical process like the shot and dark noise, the variability cannot be calculated from its mean value; it has to be measured directly. The standard deviation of the Read noise is N_r which is then squared to produce the third term in the signal to noise ratio equation.

The signal to noise equation can be modified to take into account the effect of summing a number (F) of shorter exposure frames to produce the same total exposure.

The equation for a single frame is modified as follows:

signal =

shot noise term =

dark noise term =

readout noise (unchanged) = N_r²

The total single frame noise therefore becomes

and

The SNR (short exposure frame) = 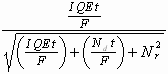----------------(2)

If we now sum F short exposure frames:

Sum signal = I QE t ie the same as for a single long exposure

To calculate the total noise we sum F of each term inside the square root ie

Sum noise =

ie the contributions from shot and dark noise are the same as for a single long exposure but the contribution from the read noise increases F times.

The SNR (stack) = -------------------------------------(3)

DOWNLOAD SPREADSHEET

We can now use equations (1,) (2), (3) to explore the effect of stacking in a numerical example where

t = 50 sec F = 100 I QE = 20 electrons/sec N_d = 5 electrons/sec N_r = 5 electrons